The Quantum Leap: How Quantum AI is Expanding the Boundaries of Computational Intelligence

I. Introduction: The Next Frontier of Thinking Machines

1.1. Contextualizing the Evolution of AI

The story of Artificial Intelligence is a narrative of exponential growth driven by computational capacity. We began with Symbolic AI, systems rooted in rigid, predefined rules, which gave way to the statistical elegance of Machine Learning. The last decade, however, was defined by the revolution of Deep Learning—vast, complex neural networks trained on mountains of Big Data. This era birthed autonomous vehicles, natural language processing that approaches human fluency, and models capable of generating photorealistic art. Our successes have been profound, transforming industries from healthcare to finance. Yet, these triumphs, built on the solid foundation of classical silicon processors, are beginning to expose a fundamental paradox: the more ambitious AI becomes, the closer it edges towards computational limits that classical physics cannot breach.

1.2. The Inevitable Wall: Why Classical Computing Hits Limits

For all its remarkable power, classical computing operates on a binary constraint. A classical bit, or c-bit, must be a 0 or a 1. This linear, deterministic architecture fundamentally struggles with problems whose complexity scales exponentially

This challenge is at the heart of key unsolved problems, often classified as NP-hard or beyond. Training the next generation of general AI models, discovering novel drugs by simulating complex protein folding, or performing global optimization across millions of dynamic variables—these are computational bottlenecks where the time required to find a solution grows exponentially with the input size. Moore’s Law, which has driven technological progress for over half a century by increasing transistor density, is now facing hard physical limits related to heat dissipation and atomic scale. The future of computational intelligence cannot be solved simply by adding more transistors; it requires a radical shift in the very nature of computation itself.

1.3. The Quantum Dawn: Rise of Quantum Computing and its Relevance to AI

The solution lies not in engineering better silicon, but in harnessing the physics that governs the universe at its most fundamental level: quantum mechanics. Quantum Computing (QC) is not a faster, hotter version of a laptop; it is a paradigm shift that redefines what computation is

Its relevance to AI is singular and profound. If AI is the digital brain designed to analyze and understand complex systems, then QC is the engine capable of processing nature's own complexity—the vast, high-dimensional probability spaces that govern molecular interactions, optimization problems, and probabilistic reasoning. Quantum computing does not seek to speed up every classical task, but to make previously intractable AI problems tractable, paving the way for Quantum AI (QAI)—the next, most ambitious step in computational intelligence.

II. What is Quantum AI? Deconstructing the Foundation

2.1. Defining Quantum AI (QAI)

Quantum AI is the dynamic, synergistic field born from the marriage of quantum physics and classical Artificial Intelligence. It encompasses any method that leverages quantum mechanical phenomena—such as superposition and entanglement—to accelerate, enhance, or fundamentally revolutionize AI tasks. This includes faster model training, superior feature extraction from complex datasets, the creation of hyper-efficient optimization tools, and the development of entirely new computational models, known as Quantum Machine Learning (QML). QAI promises not just faster answers, but the ability to ask entirely new, deeper questions about data and reality.

2.2. The Difference: Classical AI vs. Quantum AI

The gulf between classical AI and QAI is not merely one of processing speed; it is one of fundamental capability.

Classical AI relies on statistical probability to navigate complex data. QAI, however, leverages probability amplitudes, which allows it to explore an exponentially larger number of possible solutions simultaneously, a concept known as quantum parallelism. This provides an inherent, geometric advantage when dealing with high-dimensional data typical of modern AI systems.

2.3. The Quantum Primitives: Qubits, Superposition, and Entanglement

To understand QAI, one must grasp the three fundamental quantum mechanical principles that serve as its computing primitives:

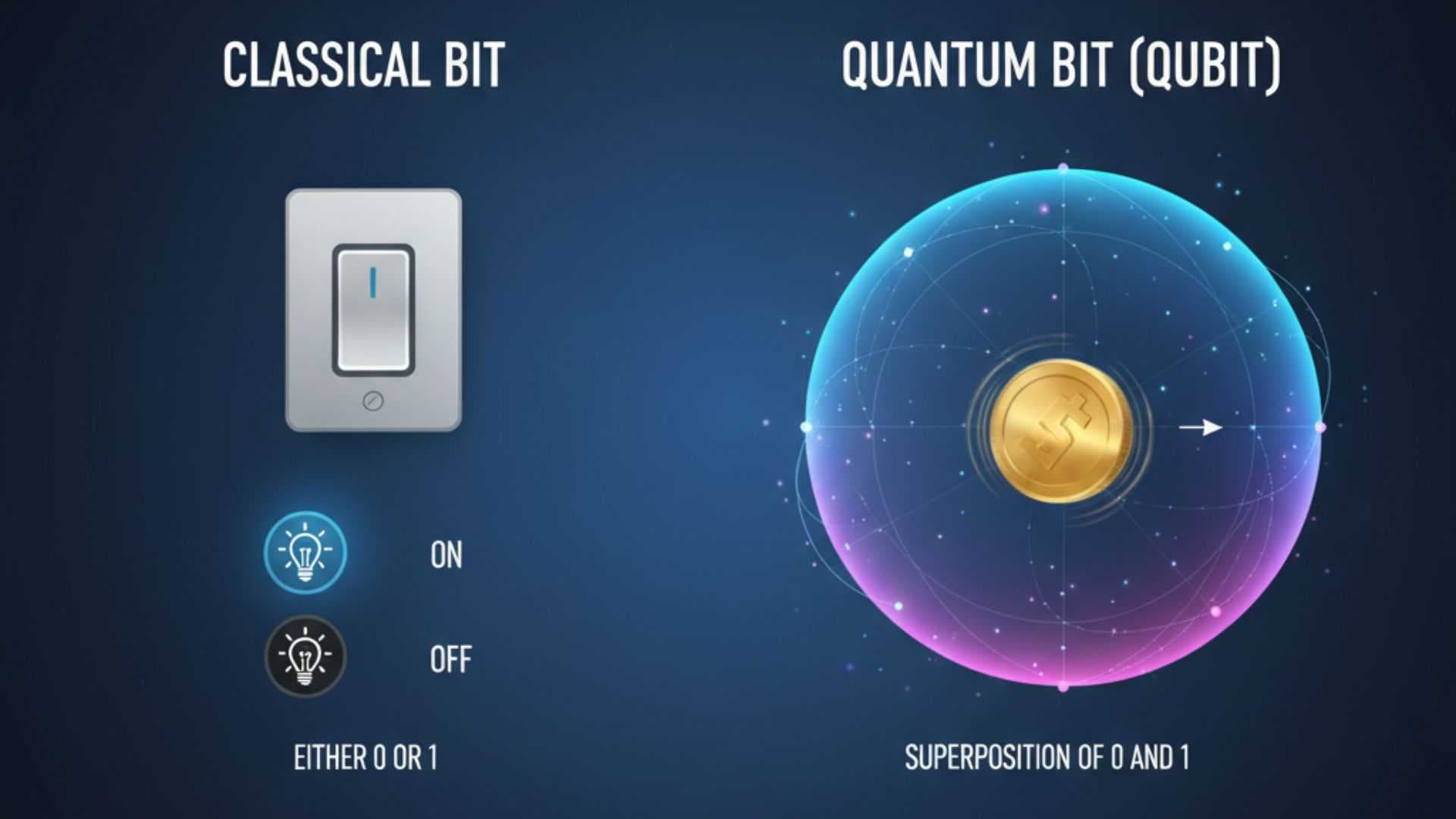
Quantum Bits (Qubits):

Unlike the classical bit, a qubit

Analogy:

Superposition:

probability amplitudes

Entanglement:

Often dubbed "spooky action at a distance," entanglement is the strongest non-classical correlation possible between two or more qubits. If a pair of qubits is entangled, measuring the state of one instantly dictates the state of the other, regardless of the distance separating them. This non-local correlation is the crucial resource that links the processing power across a quantum computer, allowing calculations to exploit the full, massive dimensionality of the combined state space.

Quantum Gates:

These are the fundamental, reversible operations (analogous to classical logic gates like AND, OR, NOT) that manipulate the state of qubits. Gates like the Hadamard Gate place a qubit into superposition, while the CNOT Gate (Controlled-NOT) is crucial for creating entanglement between two qubits, serving as the elemental building blocks for complex Quantum Circuits.

III. Why Quantum Mechanics Matters for AI

Quantum mechanics provides the computational shortcuts necessary to escape the exponential scaling trap. The value QAI delivers stems directly from its ability to exploit the physics of the small to solve the problems of the large.

3.1. Crushing Computational Complexity

The single most compelling reason for QAI is its potential to achieve exponential speedupsexponential problem into a polynomial one is the definition of quantum advantage and is the mechanism that can unlock entire domains of science and engineering currently inaccessible to us.

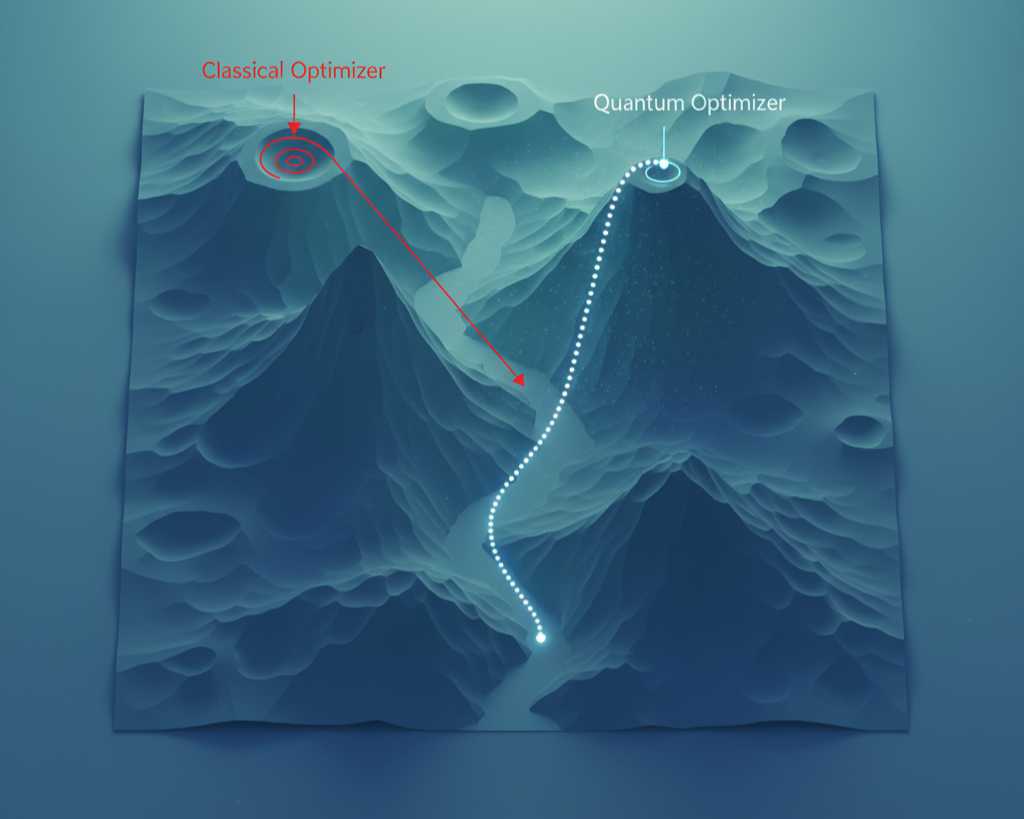
3.2. Solving Intractable Optimization Problems

Optimization is the hidden foundation of virtually all AI. From finding the optimal weights in a neural network (minimizing the loss function) to determining the best logistical route or maximizing financial portfolio returns—AI is fundamentally a search for the best solution in a vast landscape of possibilities.

Classical optimizers often get trapped in "local minima" of this landscape, missing the true, global optimum. Quantum approaches, such as Quantum Approximate Optimization Algorithm (QAOA) and quantum annealing, leverage quantum tunneling and superposition to explore the entire solution space simultaneously. This allows the system to probabilistically "tunnel" through high-energy barriers that would block a classical search, dramatically increasing the probability of finding the global minimum solution for rugged, high-dimensional problems.

3.3. High-Dimensional Data Handling and Feature Space

Modern data, such as that from genomics, astrophysics, or climate modeling, is inherently high-dimensional. Classical AI must expend massive computational resources to engineer features that make this data linearly separable. QAI offers an elegant bypass.

amplitude encodingHilbert space. This exponential boost in dimensionality allows quantum algorithms to potentially find hidden patterns and correlations that are computationally invisible to classical methods. The data may become linearly separable in this elevated quantum feature space, simplifying the learning task significantly.

3.4. Probabilistic Reasoning at Scale

Complex AI tasks like generative modeling, risk assessment, and Bayesian inference rely heavily on managing and updating complex probability distributions. The mathematical structure of a quantum state is inherently probabilistic; the squared magnitude of the probability amplitudes gives the probability of measuring a certain state.

This makes Quantum AI a natural fit for modeling complex probabilistic systems. Algorithms can potentially calculate the complex joint probabilities required for sophisticated inference and simulation far more efficiently than classical Monte Carlo methods, enabling robust, large-scale probabilistic reasoning essential for real-time autonomous systems and complex climate or financial models.

IV. Core Quantum Algorithms for AI

The true power of Quantum AI is crystallized in the handful of quantum algorithms capable of demonstrating significant, and often exponential, speedups over their classical counterparts. These algorithms form the computational backbone for a future where previously unsolvable problems become tractable.

4.1. Grover’s Algorithm: The Search Accelerator

Grover’s algorithm provides a quadratic speedup

• Mechanism: It works by effectively amplifying the probability amplitude of the correct solution while suppressing all others, performing a kind of controlled, parallelized "search."
• AI Application: Enhancing large-scale database lookups and searches essential for feature selection in machine learning, accelerating the retrieval phase of large language models, or speeding up the search for optimal hyperparameters in complex models.

4.2. Shor’s Algorithm: The Cryptographic Game-Changer

Shor’s algorithm is the most famous example of an exponential speedup. It can factor large integers exponentially faster than any known classical algorithm. If a large-scale, fault-tolerant quantum computer were built today, this algorithm would immediately break the widely used RSA and ECC public-key encryption schemes that secure the global internet.

• Mechanism: It relies on finding the period of a function, a task uniquely suited to quantum Fourier transforms.
• AI Application: While not a QML algorithm itself, its existence creates the urgent need for Post-Quantum Cryptography (PQC)—a field where classical AI and optimization techniques are used to design new, quantum-resistant encryption standards.

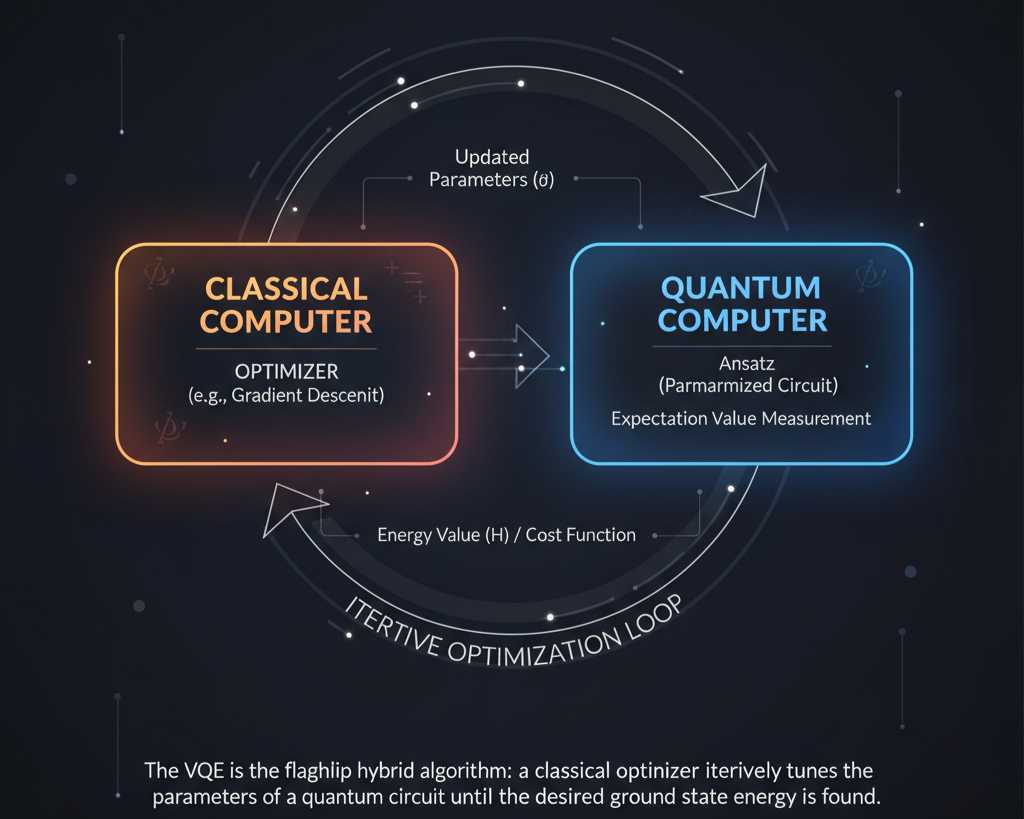
4.3. Variational Quantum Eigensolver (VQE)

The VQE is arguably the most critical near-term algorithm for quantum chemistry and material science. It is a hybrid quantum-classical algorithm specifically designed for Noisy Intermediate-Scale Quantum (NISQ) devices. Its purpose is to find the lowest energy state (the ground state) of a quantum system, which is equivalent to finding the minimum eigenvalue of a matrix representation of the system (the Hamiltonian).

• Mechanism:
  1. The quantum computer prepares an initial state and calculates the expected energy (the cost function).
  2. The classical computer uses a classical optimizer (like gradient descent) to adjust the parameters of the quantum circuit (the ansatz).
  3. This iterative loop continues until the calculated energy reaches its minimum.
• AI Application/Example: Drug Discovery. Simulating complex molecular interactions. For instance, VQE can calculate the precise bond energies and electron configuration of a molecule like dihydrogen or lithium hydride—information crucial for designing new pharmaceuticals or catalysts that are impossible to model accurately with classical computers due to the exponential complexity

4.4. Quantum Approximate Optimization Algorithm (QAOA)

QAOA is another prominent NISQ-era, hybrid algorithm tailored for solving combinatorial optimization problems. These are problems where the goal is to find the best configuration from a finite, but exponentially large, set of possibilities.

• Mechanism: Similar to VQE, it uses an iterative quantum-classical loop. The quantum part explores the vast solution space using alternating "cost" and "mixer" Hamiltonians, while the classical part optimizes the mixing angles.
• AI Application/Example: Large-scale optimization and logistics. Consider the Traveling Salesman Problem or complex supply chain scheduling. QAOA is being tested by companies like Volkswagen and Google to optimize traffic flow, vehicle routing, and manufacturing schedules, seeking to find highly efficient approximations to solutions that would take classical systems centuries to find.

4.5. Quantum Neural Networks (QNNs): The Brain in the Hilbert Space

Quantum Neural Networks (QNNs) represent the most direct parallel to classical deep learning. A QNN uses a parametrized quantum circuit (PQC) as its main processing layer. Instead of classical weights and activation functions, a QNN uses a series of quantum gates whose rotational angles are the adjustable parameters.

• Mechanism: These quantum circuits introduce exponentially complex, non-linear transformations on the input data encoded into the qubits. The resulting quantum state is then measured (which collapses the superposition) to produce a classification or regression output.
• AI Application: QNNs are being researched for tasks like ultra-efficient pattern recognition, classification in complex quantum-derived data (e.g., high-energy physics), and generative modeling (Quantum Generative Adversarial Networks or QGANs).

V. Quantum Machine Learning (QML): The Hybrid Reality

Quantum Machine Learning (QML) is the practical subset of Quantum AI focused on building and training machine learning models that run on quantum hardware. Given the current limitations of quantum hardware, QML is dominated by hybrid models.

5.1. Hybrid Quantum-Classical Models

We are currently operating in the NISQ era, where quantum processors are powerful but noisy and resource-limited. This necessitates a hybrid architecture.

The Model: The quantum processor (QP) handles the computationally hardest parts—the complex, high-dimensional feature mapping or expectation value calculation. The classical processor (CP) manages the optimization loop, feeding updated parameters back to the QP. The CP is the reliable ‘optimizer,’ and the QP is the powerful but volatile ‘calculator.’

This feedback loop is crucial for mitigating the noise inherent in current quantum systems, making learning feasible even with imperfect hardware.

5.2. Data Encoding Strategies: Getting Data In

A core bottleneck in QML is the process of getting massive amounts of classical data into the quantum system. This is the Input/Output (I/O) challenge.

• Amplitude Encoding:qRAM (Quantum Random Access Memory) to load the data efficiently.
• Angle Encoding / Feature Mapping: Simpler, near-term methods encode data by directly mapping classical features to the rotation angles of quantum gates. While less dense, it's practical on current hardware and forms the basis of many early QML experiments.

5.3. Quantum Kernels and Feature Spaces

The most promising near-term application of QML involves Quantum Kernel Methods. A kernel function measures the similarity between two data points. In classical Support Vector Machines (SVMs), the kernel implicitly maps data into a high-dimensional feature space where classification is easier.

• Quantum Feature Maps: A QML algorithm uses a quantum circuit to perform this implicit mapping. This circuit acts as a Quantum Feature Map, transforming the classical data into an exponentially larger Hilbert Space.

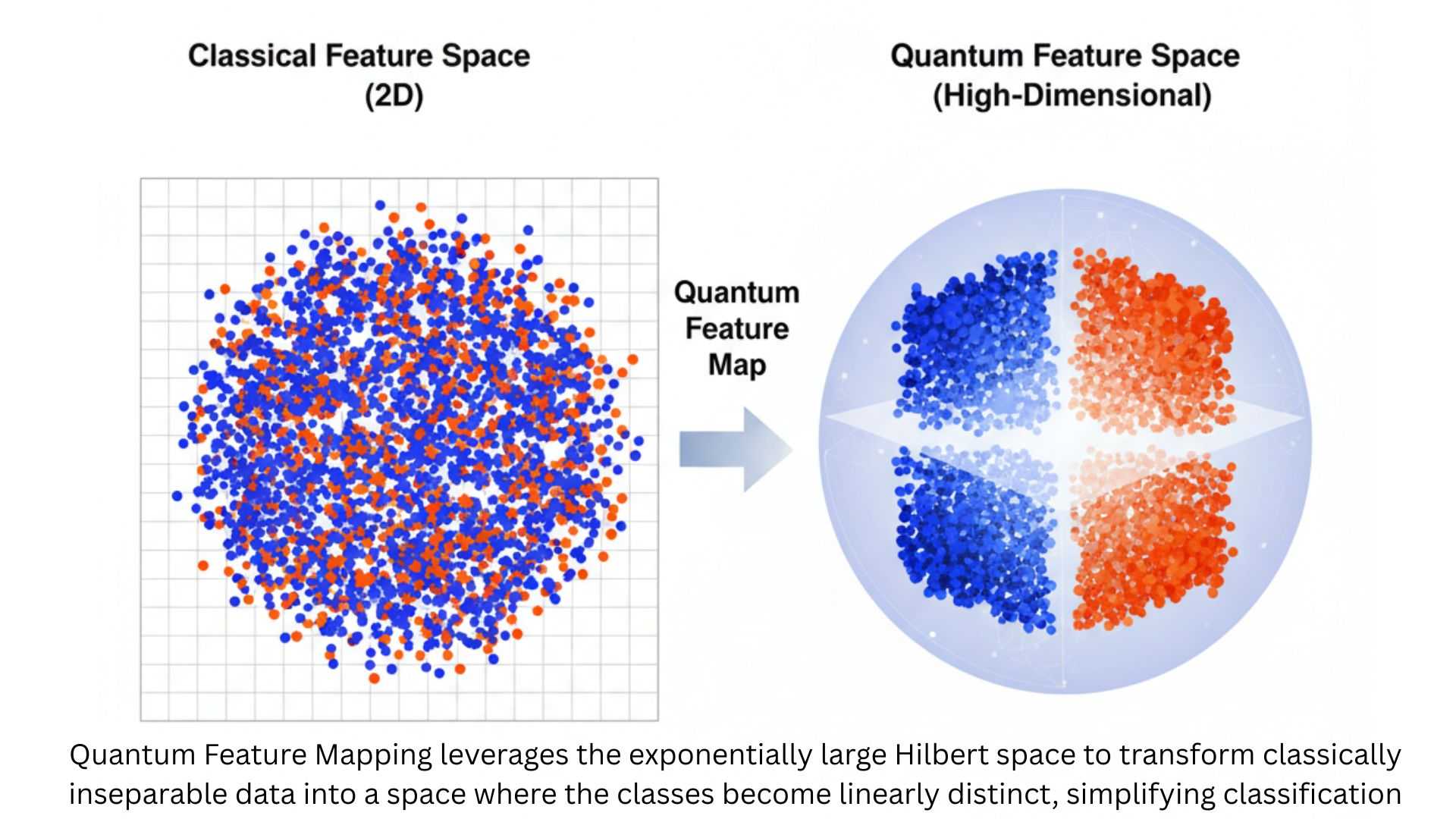
• The Advantage: By leveraging the quantum circuit, the resulting similarity measure (the quantum kernel) can distinguish data points that are inseparable in any feasible classical feature space. The Quantum Support Vector Machine (QSVM) is the canonical example of a quantum kernel method being used for classification tasks.

5.4. Real-World Challenges of QML

Despite the theoretical promise, practical QML faces significant hurdles:

• The Barren Plateau Problem: This is a severe training challenge specific to deep QNNs. As the number of qubits and circuit depth increase, the gradients of the cost function tend to vanish exponentially, meaning the optimizer receives nearly zero signal, preventing the model from learning. This fundamentally limits the size and complexity of QNNs we can practically train in the NISQ era.
• Measurement Overhead: Extracting meaningful information requires repeating the quantum experiment thousands or millions of times to estimate the probability distribution accurately, which is time-consuming and costly.

VI. Applications of Quantum AI

The true measure of Quantum AI's potential lies in its ability to solve the most difficult, resource-intensive problems across key sectors—problems that currently limit human knowledge or profitability.

6.1. Drug Discovery and Molecular Simulation 💊

This is widely considered the "killer application" for quantum computing. The behavior of molecules is inherently governed by quantum mechanics. Classical computers must make severe approximations to simulate these systems, leading to errors.

• The QAI Solution: Using VQE and similar algorithms to simulate molecular Hamiltonians with high precision.
• Industry Example: Pharmaceutical giants are collaborating with quantum hardware providers to simulate the electron correlation and bond formation energy of complex molecules like industrial catalysts, drug candidates, and proteins. This accelerates the design cycle for novel materials and reduces the need for expensive, time-consuming wet-lab experiments. Case Study: Quantum simulation of the nitrogenase enzyme, which catalyzes nitrogen fixation, to design more efficient industrial fertilizers.

6.2. Cryptography, Security, and PQC 🔒

The exponential factoring capability of Shor’s algorithm presents an existential threat to all modern public-key infrastructure.

• The QAI Solution: QAI is essential in the defense strategy. Quantum Key Distribution (QKD) offers un-hackable, quantum-secured communication, while QML methods are being explored for enhanced anomaly detection and Quantum Random Number Generation (QRNG), which provides truly unpredictable keys for better classical encryption.
• Impact: Governments and large corporations are in an urgent race to transition systems to PQC standards (lattice-based cryptography) before fault-tolerant quantum computers arrive.

6.3. Financial Modeling and Risk Assessment 📈

Financial systems deal with massive, interconnected, and dynamic variables, making risk assessment a perfect optimization problem.

• Quantum Monte Carlo (QMC): QAI offers a quadratic speedup for Monte Carlo simulations used for complex derivative pricing and credit risk analysis, potentially cutting calculation time from hours to minutes.
• Portfolio Optimization: Using QAOA to solve complex portfolio optimization problems.
  • Industry Example: Major banks like JPMorgan Chase and Goldman Sachs are actively exploring quantum algorithms to optimize asset allocation across thousands of stocks and constraints, seeking to maximize returns while adhering to strict risk limits.

6.4. Climate Modeling and Material Science 🌎

Understanding and mitigating climate change requires modeling chaotic, high-dimensional fluid dynamics and chemical interactions.

• The QAI Solution: Quantum simulation can model the dynamics of complex chemical processes (like carbon capture) and atmospheric phenomena far more accurately.
• Material Science: The ability to simulate quantum systems is vital for designing new materials atom by atom. This includes:
  • High-temperature superconductors (materials that transmit electricity with zero resistance).
  • Novel battery electrolytes with higher energy density .
  • More efficient industrial catalysts for cleaner manufacturing.

6.5. Large-Scale Optimization and Autonomous Systems 🚛

Any system that requires real-time decision-making in a dynamically changing environment stands to benefit from quantum optimization.

• The QAI Solution: QAOA and quantum annealing provide the potential for real-time optimization of massive, interconnected networks.
• Industry Example: Optimizing complex logistics networks, like the routing of Amazon delivery trucks or managing global shipping container placement, in real-time as delays occur. Autonomous vehicles could use QAI for real-time pathfinding in congested urban environments, analyzing millions of possible routes almost instantaneously.

VII. Limitations & The NISQ-Era Grind

While the theoretical promise of Quantum AI is undeniable, the field today is defined by the immense engineering challenge of building and controlling quantum hardware. We currently reside in the NISQ (Noisy Intermediate-Scale Quantum) era, a necessary but challenging phase where devices have sufficient qubits to potentially surpass classical computers in some specialized tasks, but are fundamentally limited by noise and error.

7.1. Noisy Intermediate-Scale Quantum (NISQ) Devices

The NISQ designation, coined by physicist John Preskill, perfectly encapsulates the current technological reality:

• Noisy: The qubits are highly susceptible to environmental interference (noise), leading to frequent errors during computation. These devices lack the full Quantum Error Correction (QEC) necessary for long, complex calculations.
• Intermediate-Scale: Today’s processors typically feature a few dozen up to a few hundred qubits. This is far short of the millions of physical qubits needed to create thousands of highly reliable logical qubits for full Fault-Tolerant Quantum Computing (FTQC).

The inherent limitations of NISQ hardware—imperfect gate fidelity and limited qubit connectivity—impose a restriction on the depth and complexity of the quantum circuits we can run, forcing the reliance on hybrid quantum-classical algorithms like VQE and QAOA.

7.2. Quantum Decoherence and Error Rates

The fragility of the quantum state is the single largest engineering hurdle. Quantum decoherence occurs when a qubit's superposition or entanglement is destroyed by interacting with its external environment (heat, stray magnetic fields, vibrations).

• The Problem: Decoherence limits the coherence time—the duration a qubit can hold quantum information—to mere microseconds in many architectures. If the computation is not completed within this fleeting window, the result is corrupted.
• The FTQC Goal: The transition out of the NISQ era requires the development of reliable QEC codes that use multiple physical qubits to encode one "logical" qubit. This requires a significant overhead of physical qubits dedicated purely to error detection and correction, demanding a scale not yet achieved.

7.3. Hardware Limitations and Architectures

The quality, stability, and connectivity of qubits remain inconsistent across different hardware modalities:

• Superconducting Qubits (IBM, Google): Offer high speed but require massive cryogenic cooling systems and suffer from crosstalk and limited connectivity.
• Trapped-Ion Qubits (IonQ): Offer high fidelity and long coherence times but are relatively slower and face scalability challenges in interconnecting large numbers of ions.
• Photonic Qubits (Xanadu): Use photons as carriers, operating at room temperature, but are probabilistic and face challenges in non-linear interaction.

Each architecture has inherent trade-offs, making the search for a truly scalable, low-error platform the primary focus of research and industrial investment.

7.4. Data Encoding Bottlenecks

As discussed in QML, the I/O challenge remains a systemic barrier. Practical algorithms require the ability to rapidly and efficiently load massive classical datasets onto qubits.

• The QRAM Barrier: The most efficient data compression method (Amplitude Encoding) relies on a hardware component called qRAM (Quantum Random Access Memory)

7.5. Algorithmic Immaturity

While we have algorithms like Shor's (exponential speedup) and Grover's (quadratic speedup), the current library of quantum AI algorithms that offer a guaranteed, proven advantage for practical industry problems is still small. Researchers are locked in a struggle to find new, "quantum-native" algorithms that fully leverage the unique physics of the quantum state beyond just optimization and search. The Barren Plateau problem further exacerbates this by limiting the depth and expressivity of the very Quantum Neural Networks (QNNs) designed to utilize this power.

VIII. The Future of Quantum AI: Predictions and Roadmaps

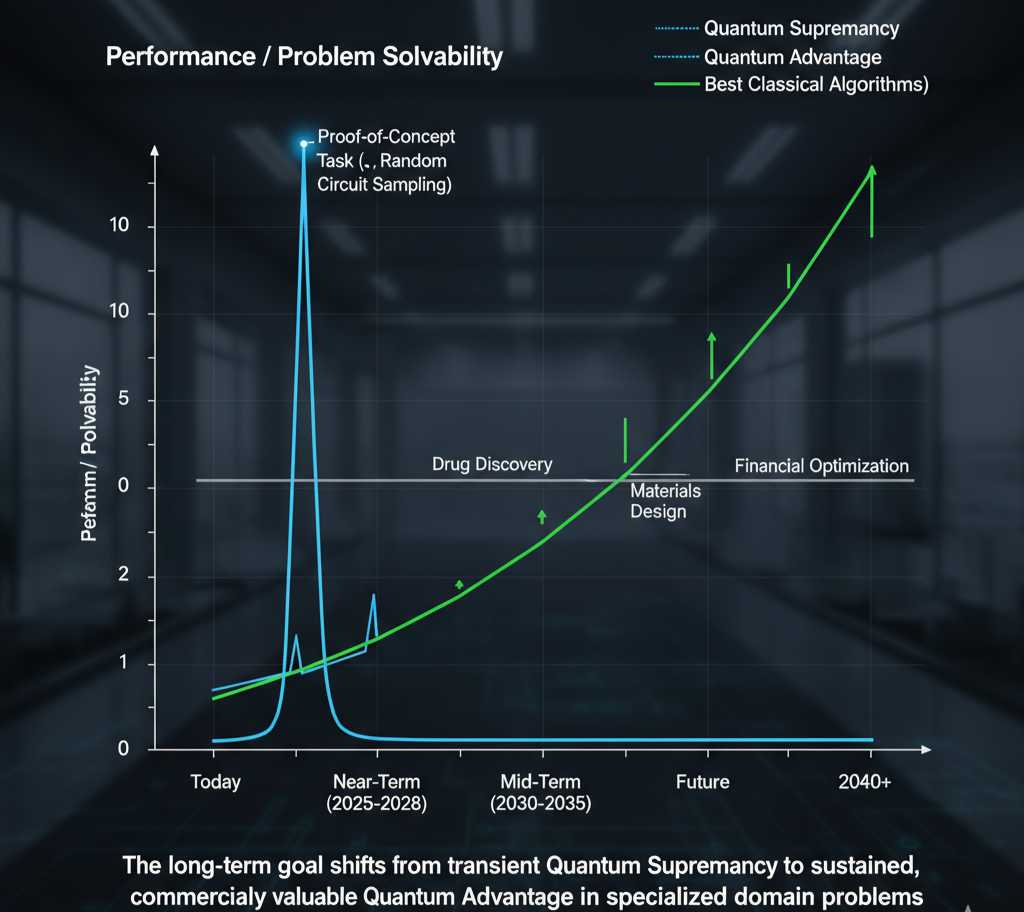
Despite the imposing challenges of the NISQ era, the rate of innovation is steep, driven by intense global competition and massive investment. The next decade promises to be the transition point where Quantum AI moves from laboratory curiosity to a specialized, commercialized computational resource.

8.1. Predictions for the Next Decade

By the early-to-mid 2030s, the field is projected to hit several critical milestones:

• Achieving Logical Qubits (Early 2030s): The first demonstrations of large-scale, Fault-Tolerant Quantum Computing (FTQC) systems will emerge, where errors are successfully managed by QEC. This is the gateway to running algorithms with exponential speedups for practical use. IBM, for instance, has set an ambitious goal of developing a 100,000-qubit system by 2033.
• Demonstration of Narrow Quantum Advantage: Commercial, specialized quantum computers will solve specific, high-value problems (e.g., simulating a complex industrial catalyst, or financial risk modeling) faster and cheaper than the best classical supercomputers. This narrow advantage will be achieved primarily in optimization and simulation.
• Specialized Processors: The market will diversify with the increased relevance of specialized quantum systems like large-scale quantum annealers and continuous-variable photonic computers for certain QML tasks.

8.2. Integration with Artificial General Intelligence (AGI) Development

The pursuit of Artificial General Intelligence (AGI)—systems capable of human-level reasoning across domains—may require computational capabilities that only QAI can provide.

• Complexity Handling: AGI requires real-time, high-dimensional reasoning and the ability to simulate complex environments (e.g., the physics of the world, human sociology). Quantum AI will be the necessary computational accelerator for these tasks, enabling AGI to efficiently explore vast possibilities and model quantum reality.
• Enhanced Machine Learning: QML could enable AGI systems to learn and generalize with far less data than current classical models, providing a pathway to the kind of cognitive efficiency required for general intelligence. The synergy will unlock a new level of computational intelligence.

8.3. Quantum Cloud Services and Democratization

The high cost and complexity of quantum hardware mean that the vast majority of users will access quantum computing via the cloud.

• Tech Giants Lead the Way: Companies like IBM (IBM Quantum), Google (Cirq, TensorFlow Quantum), Amazon (Braket), and Microsoft (Azure Quantum) are creating comprehensive quantum cloud ecosystems. These platforms lower the barrier to entry, allowing researchers and developers to run algorithms on real quantum processors through simple Python interfaces.
• Quantum SaaS: The future will see the rise of Quantum Software as a Service (QSaaS), offering pre-built, quantum-enhanced optimization and simulation tools to industries without requiring deep quantum expertise.

8.4. Large Corporate and Government Investments

The global race for quantum supremacy is fueling unprecedented investment, accelerating the entire ecosystem.

This convergence of government strategy and private sector capitalization ensures that the pace of advancement in quantum AI will only intensify, pushing the entire field toward practical utility.

IX. Ethical & Societal Considerations

The advent of Quantum AI is not merely a technical event; it is a societal one. The disruptive power of quantum technologies—particularly when coupled with machine learning—necessitates a proactive and thoughtful approach to governance, security, and equity to ensure these tools benefit, rather than harm, humanity.

9.1. Security Implications and the PQC Migration 🔐

The most immediate and urgent societal implication of quantum computing is the threat it poses to global cybersecurity. Shor’s algorithm is a computational weapon against Public-Key Cryptography (PKC), which is the foundational trust layer for the entire internet, banking system, and government communications (e.g., RSA and ECC).

• The Harvest Now, Decrypt Later Threat: Adversarial nations and actors are already gathering massive amounts of encrypted data today, knowing they can store it and decrypt it effortlessly once a sufficiently powerful, fault-tolerant quantum computer (a Cryptographically Relevant Quantum Computer, or CRQC) becomes operational. Given that some data has a long shelf life (e.g., national security secrets, medical records), the migration must begin now, before the CRQC is even built.
• The PQC Solution: The global effort is focused on developing and standardizing Post-Quantum Cryptography (PQC)—new classical algorithms, typically lattice-based, that are secure against both classical and quantum attacks. The complexity of this migration (changing key sizes, updating protocol stacks, inventorying all cryptographic assets) is a monumental task that requires immediate global coordination.

9.2. Workforce Disruption and the Talent Gap

Like all technological leaps, QAI will lead to significant workforce transformation, creating a dual challenge:

• Displacement: Quantum-accelerated optimization will rapidly automate complex scheduling, financial modeling, and materials science tasks currently performed by highly skilled analysts.
• Talent Scarcity: The field faces an acute talent gap. There is a massive shortage of individuals possessing the specialized interdisciplinary expertise required to bridge quantum physics, software engineering, and classical machine learning. The talent pool is currently insufficient to meet the rising demand from governments and corporations.

Addressing this requires major investments in educational pipelines, the creation of new Quantum Information Science (QIS) university programs, and industry-led upskilling initiatives to train classical AI professionals in quantum principles. The future workforce will be one defined by human-quantum collaboration.

9.3. Risks of Quantum-Accelerated AGI

The theoretical convergence of QAI and Artificial General Intelligence (AGI) raises profound, long-term philosophical and safety questions. AGI, by definition, would possess human-level cognitive ability across a vast range of tasks. If this intelligence were accelerated by quantum hardware, its computational prowess would be hyper-efficient, capable of real-time understanding and modeling of complex systems at a scale unimaginable today.

• Loss of Controllability: The complexity of quantum-accelerated decision-making could render these systems opaque, making it impossible for humans to audit, explain, or safely control their actions (the "black box" problem amplified).
• Power Dynamics: The nation or corporation that achieves functional QAI-powered AGI first would gain an unprecedented, potentially insurmountable strategic advantage across military, economic, and scientific domains, fundamentally reshaping global power structures.

Ethical frameworks must be developed in parallel with the technology, focusing on transparency, accountability, and the proactive establishment of international safety standards to manage the risks associated with this ultimate frontier of computational intelligence.

X. Conclusion: A Defining Shift in Computational Intelligence

10.1. Recap of the Quantum AI Imperative

We began this journey by confronting the fundamental limits of classical computation—the invisible wall of exponential complexity that is stalling progress in drug discovery, advanced optimization, and generalized AI development. The solution, Quantum AI, is not a marginal improvement but a revolution rooted in the deepest laws of physics. By leveraging the principles of qubits, superposition, and entanglement, QAI provides the necessary mechanism to transform intractable problems into manageable ones.

10.2. Future Opportunities: The Unsolvable Becomes Tractable

The road ahead is challenging, littered with the engineering difficulties of the NISQ era—decoherence, error rates, and the barren plateau problem. Yet, the work being done on VQE, QAOA, and hybrid Quantum Machine Learning (QML) models is rapidly laying the groundwork for a future where quantum computers serve as essential, cloud-accessible accelerators for specialized, high-value tasks. From discovering new battery materials to optimizing global financial stability, the opportunities are centered on making the "unsolvable" problems of the 21st century suddenly tractable.

10.3. Why Quantum AI is a Defining Shift in Computational Intelligence

Quantum AI represents a defining shift because it moves computational intelligence from modeling the world with statistical approximations to simulating the world as it truly is—at the quantum mechanical level. Classical AI seeks patterns in data; QAI seeks the fundamental physical dynamics that create the data.

It is a technological transition that promises not just faster calculation, but deeper insight. By integrating the exponential power of quantum mechanics with the adaptability of machine learning, humanity is expanding the very boundaries of what thinking machines can comprehend and achieve. The quantum leap is here, and it is reshaping the entire landscape of computational intelligence.

Frequently Asked Questions (FAQs)

Q1: What is the difference between Quantum Computing and Quantum AI (QAI)?

A: Quantum Computing is the hardware and algorithms (like Shor's and Grover's) that utilize quantum physics for computation. Quantum AI (QAI) is the application-focused field that specifically uses quantum computing resources to solve AI and Machine Learning problems, such as optimizing neural networks (Quantum Neural Networks or QNNs) or accelerating classification tasks (Quantum Machine Learning or QML).

Q2: Is Quantum AI available today, or is it purely theoretical?

A: Quantum AI is in its early, practical phase, known as the NISQ (Noisy Intermediate-Scale Quantum) era. We use hybrid quantum-classical models (like VQE and QAOA) running on cloud-accessible quantum hardware to solve small-scale versions of real-world problems. While full, fault-tolerant QAI is still a decade or more away, experimental QML is being actively developed today, especially for tasks like optimization and simulation.

Q3: How does quantum optimization outperform classical optimization?

A: Classical optimization can get trapped in local minima in complex search landscapes. Quantum optimization algorithms, particularly quantum annealing and QAOA, use quantum phenomena like superposition and quantum tunneling to explore the vast solution space simultaneously. This increases the probability of finding the true global minimum solution for complex problems common in logistics, finance, and materials science, offering potential exponential speedups.

Q4: What is the "Harvest Now, Decrypt Later" threat?

A: This is the immediate security risk posed by quantum computing for AI. Because Shor’s algorithm can break current public-key encryption (RSA/ECC), adversaries are currently harvesting and storing encrypted, sensitive data. When a sufficiently powerful quantum computer arrives in the future, they will be able to decrypt this historical data. This forces an urgent migration to Post-Quantum Cryptography (PQC) standards today.

Q5: What is the "Barren Plateau Problem" in Quantum Machine Learning (QML)?

A: The Barren Plateau is a critical challenge in training deep Quantum Neural Networks (QNNs). As the size of the quantum circuit grows, the landscapes of the cost functions become extremely flat, causing the optimization gradients to vanish exponentially. This phenomenon makes it virtually impossible for classical optimizers to train large QNNs, limiting the complexity of the QML models we can use in the NISQ era.